Understanding The Meaning Of Denominator: A Comprehensive Guide

The term "denominator" holds significant importance in mathematics and various real-world applications. It is fundamental to understanding fractions, ratios, and proportions, which are essential concepts in numerous fields including finance, engineering, and everyday problem-solving. This article aims to explore the meaning of the denominator, its applications, and its relevance in various contexts.

In this comprehensive guide, we will delve deep into the definition of a denominator, how it functions in mathematical expressions, and its practical applications. Additionally, we will provide insights into how the concept of the denominator is utilized in real life, making it an essential topic for students, educators, and professionals alike.

So, whether you are a student looking to grasp basic mathematical concepts or a professional seeking to refresh your knowledge, this article will equip you with valuable insights into the meaning of the denominator and its significance in mathematics and beyond.

Table of Contents

• 1. Definition of Denominator
• 2. The Mathematical Function of a Denominator
• 3. Real-World Applications of Denominator
• 4. Denominator in Fractions
• 5. Denominator in Ratios
• 6. Denominator in Proportions
• 7. Importance of Denominator in Education
• 8. Conclusion

1. Definition of Denominator

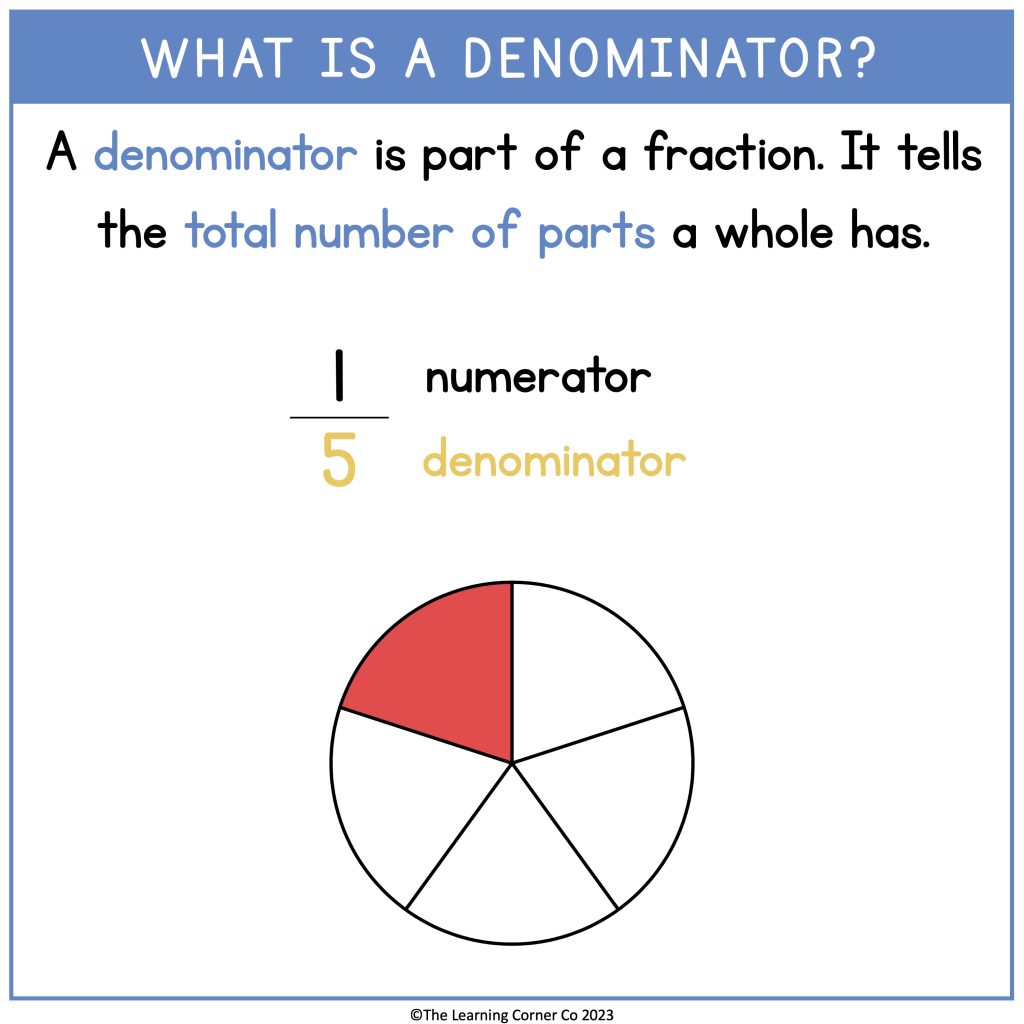
The denominator is the bottom part of a fraction, which represents the total number of equal parts into which a whole is divided. In the fraction ¾, the number 4 is the denominator, indicating that the whole is divided into 4 equal parts.

Understanding the denominator's role is crucial for grasping how fractions work. It helps in determining the value of the fraction in relation to the whole. The denominator also plays a vital role in operations involving fractions, such as addition, subtraction, multiplication, and division.

2. The Mathematical Function of a Denominator

The denominator serves several mathematical functions, including:

• Determining the size of the parts into which a whole is divided.
• Providing a basis for comparison between different fractions.
• Facilitating arithmetic operations involving fractions.

2.1 Comparison of Fractions

To compare fractions, it is essential to consider the denominators. Fractions with the same denominator can be easily compared by looking at their numerators, while fractions with different denominators require finding a common denominator.

2.2 Arithmetic Operations

When performing arithmetic operations with fractions, the denominator plays a crucial role in determining the outcome. For example:

• **Addition and Subtraction:** Fractions must have a common denominator to be added or subtracted.
• **Multiplication:** The denominators are multiplied together when multiplying fractions.
• **Division:** The reciprocal of the second fraction is used, flipping the denominator.

3. Real-World Applications of Denominator

The concept of a denominator extends beyond mathematics into various real-world applications, including:

• **Finance:** Understanding interest rates and loan terms.
• **Cooking:** Adjusting recipes based on servings.
• **Statistics:** Calculating averages and probabilities.

4. Denominator in Fractions

Fractions are a representation of parts of a whole, and the denominator is key to understanding their value. The denominator indicates how many equal parts the whole is divided into. For example, in the fraction ⅗, the denominator 5 tells us that the whole is divided into 5 equal parts, and the numerator 3 indicates how many of those parts we are considering.

5. Denominator in Ratios

In ratios, the denominator serves to compare two quantities. For instance, in the ratio 2:3, the denominator (3) represents the total parts in the second quantity. Understanding ratios is crucial in various fields, including finance, where ratios can indicate profitability or efficiency.

6. Denominator in Proportions

Proportions are equations that express the equality of two ratios. The denominators in these ratios are essential for establishing the relationship between the two quantities. For example:

• If a/b = c/d, then ad = bc, where a and c are numerators and b and d are denominators.

7. Importance of Denominator in Education

Understanding the concept of the denominator is vital in education, particularly in mathematics. It lays the foundation for more complex mathematical concepts and helps students develop critical thinking and problem-solving skills.

Educators often emphasize the importance of mastering fractions and the role of the denominator in various mathematical operations. This foundational knowledge is crucial for students as they progress to higher levels of mathematics.

8. Conclusion

In summary, the denominator is a fundamental concept in mathematics, essential for understanding fractions, ratios, and proportions. Its significance extends to real-world applications in finance, cooking, and statistics, making it a crucial topic for students and professionals alike.

We encourage readers to engage with this topic further by commenting below, sharing this article, or exploring more of our resources on mathematical concepts.

References

• Mathematics for the Nonmathematician by Morris Kline
• A First Course in Probability by Sheldon Ross
• Understanding and Using Mathematics by David A. Santos

Thank you for reading! We hope you found this article informative and insightful. We invite you to return for more articles on mathematical concepts and their applications.